THE ORIGIN OF NUMERALS


The graphical origin of the Roman numbers   ©1992-2011, Sarcone & Waeber | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Other original systems of numeration | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
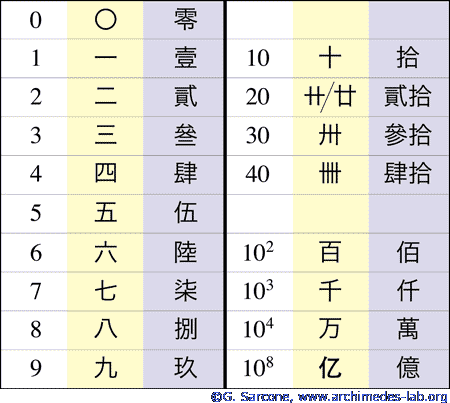
| Chinese and Japanese contributions | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Monday, 25 February 2013
Origin Of Numerals
Sunday, 24 February 2013
Gaussian Integers
GAUSSIAN INTEGERS
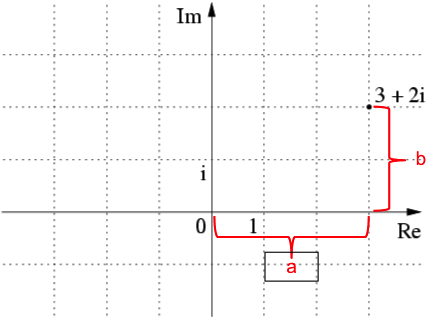

Gaussian integers can be visualized in the complex plane, with their real components on the horizontal axis, and their imaginary components orthogonal along the vertical axis.
[This post is targeted at a level 3 student who has some familiarity with complex numbers.]
Gaussian integers are complex numbers of the form 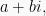 where
where  and
and  are integers. For example,
are integers. For example,  are all Gaussian integers, while
are all Gaussian integers, while  ,
, 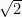 , and
, and 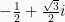 are not. One can add, subtract and multiply Gaussian integers just like all other complex numbers. For example:
are not. One can add, subtract and multiply Gaussian integers just like all other complex numbers. For example:
Addition: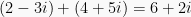 ,
,
Subtraction: ,
,
Multiplication: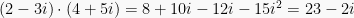 .
.
Addition:
Subtraction:
Multiplication:
As you can see, the result will again be a Gaussian integer. However, if you try to divide two Gaussian integers, the result will not always be a Gaussian integer:
Division: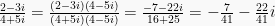 .
.
Division:
Like all complex numbers, Gaussian integers have the following properties:
1. The conjugate of 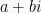 is
is  , which is again a Gaussian integer.
, which is again a Gaussian integer.
2. The norm of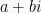 is
is 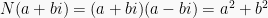 , which is a non-negative integer.
, which is a non-negative integer.
3. The absolute value of a Gaussian integer is the (positive) square root of its norm: .
.
4. There are no positive or negative Gaussian integers, and one cannot say that one is less than another. One can, however, compare their norms.
2. The norm of
3. The absolute value of a Gaussian integer is the (positive) square root of its norm:
4. There are no positive or negative Gaussian integers, and one cannot say that one is less than another. One can, however, compare their norms.
We say that a Gaussian integer  is a unit, if
is a unit, if  is also a Gaussian integer. The only units are
is also a Gaussian integer. The only units are 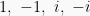 .
.
A Gaussian integer  is a multiple of a Gaussian integer
is a multiple of a Gaussian integer  if
if  for some Gaussian integer
for some Gaussian integer  . In this case we say that
. In this case we say that  divides
divides 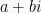 , and use the notation
, and use the notation  .
.
A Gaussian integer is called prime, if it is not equal to a product of two non-unit Gaussian integers. It is called composite otherwise. Clearly, multiplying by a unit does not change the primality. Note that the same definition for the usual integers implies that  is a prime integer. This may seem a bit strange, but no other definition makes sense for the Gaussian integers. (Keep in mind that there is no such thing as a positive Gaussian integer!) Note that a number may be prime as a usual integer, but composite as a Gaussian integer, for example
is a prime integer. This may seem a bit strange, but no other definition makes sense for the Gaussian integers. (Keep in mind that there is no such thing as a positive Gaussian integer!) Note that a number may be prime as a usual integer, but composite as a Gaussian integer, for example  .
.
There are three kinds of Gaussian primes:
1) . They are all the same up to multiplication by a unit, so we can say
. They are all the same up to multiplication by a unit, so we can say  where
where  is a unit.
is a unit.
2)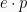 , where
, where 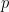 is a usual prime (
is a usual prime (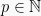 ), and
), and 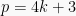 .
.
3) or
or 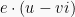 , where
, where  and
and  are natural numbers such that
are natural numbers such that  for a prime
for a prime  ,
,  . Such
. Such  and
and  exist, and are unique, up to switching
exist, and are unique, up to switching  and
and  , for every prime
, for every prime  . This classical result is called the Fermat Two Squares Theorem. It was noticed and announced by Pierre Fermat in 1640 and first proven by Leonhard Euler in 1747.
. This classical result is called the Fermat Two Squares Theorem. It was noticed and announced by Pierre Fermat in 1640 and first proven by Leonhard Euler in 1747.
1)
2)
3)
For those who had learned some abstract algebra, the algebraic properties of Gaussian integers (usually denoted by ![{\mathbb Z}[i] {\mathbb Z}[i]](http://s0.wp.com/latex.php?latex=%7B%5Cmathbb+Z%7D%5Bi%5D+&bg=f9f9f9&fg=000000&s=0) ) make it a commutative ring, moreover, a domain. Furthermore, just like the usual integers, all Gaussian integers can be decomposed into a product of Gaussian primes, uniquely up to units. The formal way of saying this is that
) make it a commutative ring, moreover, a domain. Furthermore, just like the usual integers, all Gaussian integers can be decomposed into a product of Gaussian primes, uniquely up to units. The formal way of saying this is that ![{\mathbb Z}[i] {\mathbb Z}[i]](http://s0.wp.com/latex.php?latex=%7B%5Cmathbb+Z%7D%5Bi%5D+&bg=f9f9f9&fg=000000&s=0) is a unique factorization domain (UFD for brevity).
is a unique factorization domain (UFD for brevity).
The classification of Gaussian primes is far from obvious, and so is the unique factorization property. (Speaking of which, do you know how to prove it for the usual integers? You know it to be true from experience, but it is actually not easy to prove!) These theorems will be proven in the upcoming post.
Worked Examples
1. Suppose  is a usual integer. Show that a Gaussian integer
is a usual integer. Show that a Gaussian integer 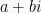 is a multiple of
is a multiple of 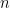 if and only if both
if and only if both  and
and  are multiples of
are multiples of 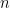 .
.
Solution: By definition, one Gaussian integer is a multiple of the other if and only if their ratio is also a Gaussian integer. Observe that  , so
, so  and
and  are integers, which means that both
are integers, which means that both  and
and 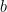 are multiples of
are multiples of  .
.
2. Suppose 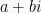 is a multiple of
is a multiple of  . Show that
. Show that  is a multiple of
is a multiple of  .
.
Solution: If  , then
, then  . Therefore,
. Therefore,


Because and
and  are integers,
are integers,  is an integer.
is an integer.
Because
This is the multiplicative property of the norm, which was mentioned in Complex Numbers Test Yourself 2.
3. Decompose 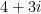 into a product of primes.
into a product of primes.
Solution: Because 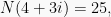 the norm of any prime that divides
the norm of any prime that divides 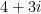 must divide
must divide  . Looking at the classification of primes, because
. Looking at the classification of primes, because 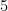 is
is 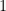 modulo
modulo  and
and 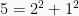 , there are two such primes, up to units:
, there are two such primes, up to units:  and
and  . Dividing
. Dividing 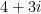 by
by  , we get
, we get  which is not a Gaussian integer. Dividing
which is not a Gaussian integer. Dividing 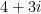 by
by  , we get
, we get  . So
. So 
4. Suppose a Gaussian integer  divides a Gaussian integer
divides a Gaussian integer 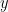 . Show that
. Show that  divides
divides 
Solution: From Complex Numbers – Worked Example 3, we know that conjugate distributes across multiplication, hence if  , then
, then  .
.
Give a Try & Test Yourself
1. Show that  and
and 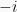 are Gaussian units and there are no other Gaussian units.
are Gaussian units and there are no other Gaussian units.
2. Find two Gaussian integers that have the same norm and are NOT multiplies of each other, hence the converse of the Example 2 is not true.
3. Show that 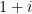 is a prime. Hint: Norm.
is a prime. Hint: Norm.
4. Show that every prime integer of the form 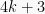 is also a Gaussian prime.
is also a Gaussian prime.
Subscribe to:
Posts (Atom)