Friday 7 June 2013

Image Of A Number

Image of a Number

The image of a number is constructed in the way that the image contains as many angles (curve) as the value number . For example , consider zero which does not contain any angle (curve) as that of its value .... But currently most of us are not using the actual image to denote the numbers .

Tuesday 2 April 2013

The Mysterious Zero / Infinity

THE MYSTERIOUS ZERO / INFINITY

Zero is behind all of the big puzzles in physics. In thermodynamics a zero became an uncrossable barrier: the coldest temperature possible. In Einstein's theory of general relativity, a zero became ablack hole, a monstrous star that swallows entire suns and can lead us into new worlds. The infinite density of the black hole represents a division by zero. The big bang creation from the void is a division by zero. In quantum mechanics, the infinite energy of the vacuum is a division by zero and is responsible for a bizarre source of energy -- a phantom force exerted by nothing at all. Yet dividing by zero destroys the fabric of mathematics and the framework of logic -- and threatens to undermine the very basis of science.

The biggest challenge to todays physicists is how to reconcile general relativity and quantum mechanics. However, these two pillars of modern science were bound to be incompatible. "The universe of general relativity is a smooth rubber sheet. It is continuous and flowing, never sharp, never pointy. Quantum mechanics, on the other hand, describes a jerky and discontinuous universe. What the two theories have in common -- and what they clash over -- is zero." "The infinite zero of a black hole -- mass crammed into zero space, curving space infinitely -- punches a hole in the smooth rubber sheet. The equations of general relativity cannot deal with the sharpness of zero. In a black hole, space and time are meaningless."

"Quantum mechanics has a similar problem, a problem related to the zero-point energy. The laws of quantum mechanics treat particles such as the electron as points; that is, they take up no space at all. The electron is a zero-dimensional object, and its very zerolike nature ensures that scientists don't even know the electron's mass or charge." But, how could physicists not know something that has been measured? The answer lies with zero. According to the rules of quantum mechanics, the zero-dimensional electron has infinite mass and infinite charge. As with the zero-point energy of the quantum vacuum, "scientists learned to ignore the infinite mass and charge of the electron. They do this by not going all the way to zero distance from the electron when they calculate the electron's true mass and charge; they stop short of zero at an arbitrary distance. Once a scientist chooses a suitably close distance, all the calculations using the "true" mass and charge agree with one another." This is known as renormalization -- the physicist Dr. Richard Feynman called it "a dippy process."

The leading approach to unifying quantum theory and general relativity is string theory. In string theory each elemental particle is composed of a single string and all strings are identical. The "stuff" of all matter and all forces is the same. Differences between the particles arise because their respective strings undergo different resonant vibrational patterns -- giving them unique fingerprints. Hence, what appear to be different elementary particles are actually different notes on a fundamental string. In string theory zero has been banished from the universe; there is no such thing as zero distance or zero time. Hence, all the infinity problems of quantum mechanics are solved.

But, there is a price that we must pay to banish zero and infinity. The size of a typical string in string theory is the Planck length, i.e., about 10^-33 centimeters. This is over a thousand trillion times smaller that what the most advanced particle detection equipment can observe. Are these unifying theories, that describe the centers of black holes and explain the singularity of the big bang, becoming so far removed from experiment that we will never be able to determine their correctness? The models of the universe that string theorists and cosmologists develop might be mathematically precise, beautiful and consistent and might appear to explain the nature of the universe -- and yet be utterly wrong. Scientific models/theories, philosophies, and religions will continue to exist and be refined. However, because of zero and infinity, we can never have "proof". All that science can know is that the cosmos was spawned from nothing, and will return to the nothing from whence it came.

Friday 15 March 2013

Origin Of Zero & Infinity

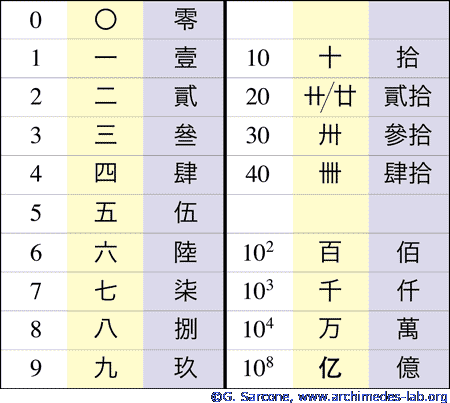
Origins of Zero

We're used to seeing it as a nothing, or even part of the code on a barcode label . But zero is probably the most complicated number in existence. It has stumped amateur math students as well as genius mathematicians since the concept of math was first developed.

Zero first appeared in the middle of the 2^nd millennium BCE when the Babylonian math system included it. Ancient Greeks were unsure about the existence of the number. It wasn’t until 9^th century India that zero began being regarded as a real number, and not a symbol for separating positive and negative numbers.

Why Dividing by Zero Can Get You into Trouble

Put simply, you run into trouble dividing by zero because zero actually can’t be divided by anything. However, people assume that you actually get a result when you divide by zero because they assume that the answer is zero. They forget the distinction - an invalid math operation is invalid, and it certainly does not equal zero.

Is Zero Either Positive or Negative?

Since zero is the marking point between negative and positive numbers, it’s neither. It has no real value so it can’t be positive or negative.

Is Zero an Even or Odd Number?

Zero is an even number. Even numbers are any number that is evenly divisible by 2. As zero divided by 2 is zero, it’s an even number.

Is 1 a Number or Just a "Unit" for Counting?

It’s actually both. One is used as both a real number as well as a unit for counting. A unit of counting means most default measurements for things in mathematics. For example, in a line segment, the default unit length is always 1.

Origin of Infinity and its Symbol

The term “Infinity” refers to several concepts. In philosophy, it means something going on forever, without end. In math, it’s used as a real number. The symbol of infinity is a sideways figure 8. However, the symbol is somewhat of a mystery because its precise origin is unknown. Though it existed many years before, it is most commonly credited to John Wallis in 1665 when he wrote De sectionibus conicis.

Other Apparent Difficulties with Zero

Most mathematicians note that what makes zero so difficult to deal with is the fact that it’s not even really a true number. They propose that it’s just a concept. It’s a way to begin measuring a set of numbers, but since zero is technically nothing, it remains a concept rather than anything concrete.

Descartes' Representations of Numbers

Rene Decartes’ mathematical work is some of the most influential ever. His work applying infinitesimal calculus to the tangent line problem allowed that branch of mathematics to rapidly progress, eventually allowing Newton to make his mark on calculus. His rule of signs is also the most widely-used method of determining the number of negative and positive roots of a polynomial. This representations of numbers changed how math was done forever.

Pi Day & History Of Pi π

Pi Day

Pi Day is celebrated on March 14th (3/14) around the world. Pi (Greek letter “π”) is the symbol used in mathematics to represent a constant — the ratio of the circumference of a circle to its diameter — which is approximately 3.14159.

Pi has been calculated to over one trillion digits beyond its decimal point. As an irrational and transcendental number, it will continue infinitely without repetition or pattern. While only a handful of digits are needed for typical calculations, Pi’s infinite nature makes it a fun challenge to memorize, and to computationally calculate more and more digits. Many of us measure the value of 22/7 as π .
but actually the value of 22/7 is nearly o.oo13 more than the actual value of π .

History

Antiquity

The Great Pyramid at Giza, constructed c. 2589–2566 BC, was built with a perimeter of about 1760 cubits and a height of about 280 cubits; the ratio 1760/280 ≈ 6.2857 is approximately equal to 2π ≈ 6.2832. Based on this ratio, some Egyptologists concluded that the pyramid builders had knowledge of π and deliberately designed the pyramid to incorporate the proportions of a circle. Others maintain that the suggested relationship to π is merely a coincidence, because there is no evidence that the pyramid builders had any knowledge of π, and because the dimensions of the pyramid are based on other factors.

The earliest written approximations of π are found in Egypt and Babylon, both within 1 percent of the true value. In Babylon, a clay tablet dated 1900–1600 BC has a geometrical statement that, by implication, treats π as 25/8 = 3.1250. In Egypt, the Rhind Papyrus, dated around 1650 BC, but copied from a document dated to 1850 BC has a formula for the area of a circle that treats π as (16/9)2 ≈ 3.1605.

In India around 600 BC, the Shulba Sutras (Sanskrit texts that are rich in mathematical contents) treat π as (9785/5568)2 ≈ 3.088. In 150 BC, or perhaps earlier, Indian sources treat π as

≈ 3.1622.

Two verses in the Hebrew Bible (written between the 8th and 3rd centuries BC) describe a ceremonial pool in the Temple of Solomon with a diameter of ten cubits and a circumference of thirty cubits; the verses imply π is about three if the pool is circular. Rabbi Nehemiah explained the discrepancy as being due to the thickness of the vessel. His early work of geometry, Mishnat ha-Middot, was written around 150 AD and takes the value of π to be three and one seventh.

Monday 25 February 2013

Origin Of Numerals

THE ORIGIN OF NUMERALS

Today's numbers, also called Hindu-Arabic numbers, are a combination of just 10 symbols or digits: 1, 2, 3, 4, 5, 6, 7, 8, 9, and 0. These digits were introduced in Europe within the XII century by Leonardo Pisano (aka Fibonacci), an Italian mathematician. L. Pisano was educated in North Africa, where he learned and later carried to Italy the now popular Hindu-Arabic numerals.
Hindu numeral system is a pure place-value system, that is why you need a zero. Only the Hindus, within the context of Indo-European civilisations, have consistently used a zero. The Arabs, however, played an essential part in the dissemination of this numeral system.

Numerals, a time travel from India to Europe
The discovery of zero and the place-value system were inventions unique to the Indian civilization. As the Brahmi notation of the first 9 whole numbers...

However, the first Western use of the digits, without the zero, was reported in the Vth century by Beothius, a Roman writer. Beothius explains, in one of his geometry books, how to operate the abacus using marked small cones instead of pebbles. Those cones, upon each of which was drawn the symbol of one of the nine Hindu-Arabic digits, were called apices. Thus, the early representations of digits in Europe were called “apices”. Each apex received also an individual name: Iginfor 1, Andras for 2, Ormis for 3, Arbas for 4, Quimas (or Quisnas) for 5 , Caltis (or Calctis) for 6, Zenis (or Tenis) for 7, Temenisa for 8, and Celentis (or Scelentis) for 9. The etymology of these names remains unclear, though some of them were clearly Arab numbers. The Hindu-Arabic-like figures reported by Beothius were reproduced almost everywhere with the greatest fantasy! (see below)

Before adopting the Hindu-Arabic numeral system, people used theRoman figures instead, which actually are a legacy of the Etruscan period. The Roman numeration is based on a biquinary (5) system.
To write numbers the Romans used an additive system: V + I + I = VII(7) or C + X + X + I (121), and also a substractive system: IX (Ibefore X = 9), XCIV (X before C = 90 and I before V = 4, 90 + 4 = 94). Latin numerals were used for reckoning until late XVI century!

The graphical origin of the Roman numbers
roman number historic

Other original
systems of numeration

Other original systems of numeration were being used in the past. The "Notae Elegantissimae" shown below allow to write numbers from 1 to 9999. They are useful as a mnemotechnic aid, e.g. the symbol K in the example may mean 1414 (the first 4 figures of the square root of 2).

Chinese and Japanese
contributions

The Ba-Gua trigrams (pron. pah-kwah, 八卦) and the Genji-Kopatterns (源氏香), antique Chinese and Japanese symbols, are strangely enough related to mathematics and electronics. If all the entire lines of the trigrams (^___) are replaced with the digit 1 and the broken lines (^{_ _}) with the digit 0, each Ba Gua trigram will then represent a binary number from 0 to 7. You can also notice that each number is laid in front of its complementary: 0<>7, 1<>6, 2<>5, etc.

Write "a", "b", "c", "d" and "e" under the five small red sticks of each Genji-Ko pattern. By doing so, you will have the 52 manners to CONNECT 5 variables in boolean algebraics. The linked sticks form a "conjunction" (AND, .), and the isolated sticks or groups of sticks form a "disjunction" (OR, +). The pattern at the top left represents:
[("a" and "d") or ("b" and "e") or "c"]

How did the Mayas represent numbers?

The Mayas, as well as the Aztecs, used a vigesimal (20) numeration. They developed 3 sets of different graphical notations to represent numbers: a) with strokes and dots, b) anthropomorphic figures, c) symbols.

a) The Mayan base-20 numeral system
mayan numerals

b) The figures shown below indicate numbers from 0 to 10

Chinese Numbers

The Peculiarity of the Chinese Numeral Notation

The Chinese use three numeral systems: the Hindu-Arabic numerals, along with two indigenous numeral systems, one for everyday writing (simple numerals), and another one for use in commercial or financial contexts (complex numerals). These last ones are used on checks and other transaction forms because they are much more difficult to alter. Actually, they are the equivalent of writing 'one', 'two', 'three', etc., rather than 1, 2, 3...
In the chart below, the first column features European or Hindu-Arabic numerals; the second one, the standard Chinese equivalent (simple numerals); and the third column, the "capital" Chinese characters (complex numerals).

The Chineses also had several other ways to represent numbers. The strange geometric figures shown below indicate the numbers 1 through 10. This numeration style - named shang fang da zhuan - is still used in official seals.

Early Egyptian Fractions

'Horus eye' or udjat was used to transcribe unit measures of capacity for grains, as you can see below each part of the eye represents a value in binary unit fraction (fig. 1). The Egyptians were also the inventors of the fraction bar. The numerator 1 and the bar were represented by a graphical symbol suggesting an open mouth; they used to note the denominators of the fraction under this symbol (fig. 2).

Did you know that the Romans too could transcribe unit fractions? E.g. to record 1/2 they used the letter S (semis). Knowing that, what represents SIX? Obviously not 6, but 8.5 (=10-1-0.5)!

$egyptian binary fractions$

The Origin of the Numbers' Names

Numbers 1 through 10 in Various Writing Systems

Indo-European Heritage

The number names in most European languages take their origin from the Indo-European language. Although various numeration systems have been used (duodecimal, vigesimal and sexagesimal numerations), the decimal system survived all of them. However, we can find traces of the vigesimal system in some French, Danish and Basque number names.

Numbers in some early European languages

	Languages using a decimal system				using a vigesimal system
	Indo-European	Sanskrit	Etruscan	Latin	Gaulish (old celt)
1	oin- (-os, -a, -om), sem-	eka (-ah, -a, -am)	thu	unus, -a, -um	un
2	dwo(u) m., dwoi f., n.	dva (dvau, dve, dve)	zal, (e)sal	duo, -ae, o	duo
3	treyes m., tisores f., tri n.	tri (trayah, trini, tisras)	ci	tres, tria n.	tri
4	kwetwores, kwetesres f.	(e)catur (eka+tri?)	sà	quattuor (quattuora n.)	petuor
5	penkwe	panca (orig. "fist"?)	mach	quinque	pinp, pemp
6	seks, sweks	sas	huth	sex	suex
7	septem	sapta	semph (?)	septem	sextan
8	okto	asta	cezp (?)	octo	oxtu
9	newn	nava (orig. "1 left..."?)	nurph- (?)	novem	naun
10	dekem	dasa (orig. "2 hands"?)	sar, zar	decem	decan
17	septemdekem	saptadasa	ci-em zathrum (20-3)	septemdecim	septandecan
18	oktodekem	astadasa	esl-em zathrum	duodeviginti (20 - 2)	oxtudecan
19	newndekem	unavimsati (20-1)	thun-em zathrum	undeviginti (20 - 1)	naudecan
20	wikemti (fromdwidekomt)	vimsati	zathrum	viginti (>vinti, vulg.)	ugant
30	trikomte (3x10)	trimsat	cialch, cealch	triginta	decan ugant(ic) (10+20)
40	kwetworkomte (4x10)	catvarimsat	sealch	quadraginta	duogant(ic) (?) (2x20)
50	penkwekomte (5x10)	pancasat	muvalch	quinquaginta	decan duogant (10+2x20)
60	seks-komte (6x10)	sasti	huthalch	sexaginta	triugant(ic) (?) (3x20)
70	septemkomte (7x10)	saptati	semphalch	septuaginta	decan triugant (?) (10+3x20)
80	oktokomte (8x10)	asiti	cezpalch (?)	octoginta	petorugant(ic) (?) (4x20)
90	newnkomte (9x10)	navati	nurphalch (?)	nonaginta	decan petorugant (10+4x20)
100	kemton	satam		centum	cant(on)
1000	(smi)gheslom	dasa satani, sahasram		mille, milia (meille, arch.)	mille
0		suna		zephyrum (lat. med.)

Numbers in some modern European languages

	Languages using a decimal system		using both decimal + vigesimal	using a vigesimal system
	Italian	English	French	Danish	Basque
1	uno	one	un	een	bat
2	due (doi)	two	deux	to	ni
3	tre	three	trois	tre	hiru
4	quattro	four (from fidwor)	quatre	fire	lau
5	cinque	five (from fimf)	cinq	fem	bortz
6	sei	six	six	seks	sei
7	sette	seven	sept	syv	zapzi
8	otto	eight	huit (orig. vit)	otte	zortzi
9	nove	nine	neuf	ni	bederatzi
10	dieci	ten	dix	ti	hamar
11	undici	eleven (from ainlif: 1 left over)	onze	elleve	hameka
12	dodici	twelve (twalif: 2 left over)	douze	tolv	hamabi
17	diciassette	seventeen	dix-sept	sytten	hama-zapzi
18	diciotto	eighteen	dix-huit	atten	hama-zortzi
19	diciannove	nineteen	dix-neuf	nitten	hama-bederatzi
20	venti	twenty (a score)	vingt	tyve	hogoi
30	trenta	thirty	trente	tredive	hogoi ta hamar (20+10)
40	quaranta	forty	quarante	fyrre	berrogoi (2x20)
50	cinquanta	fifty	cinquante	halvtreds (2.5 x "20")	berrogoi ta hamar (2x20+10)
60	sessanta	sixty	soixante	tres (3 x "20")	hirur hogoi (3x20)
70	settanta	seventy	soixante-dix (60+10)	halvfyerds (3.5 x "20")	hirur hogoi ta hamar (...+10)
71	settantuno	seventy one	soixante-onze (60+11)	enoghalvfyerds	hirur hogoi ta hameka (+11)
80	ottanta	eighty	quatre-vingts (4x20)	firs (4 x "20")	laurogoi (4x20)
90	novanta	ninety	quatre-vingt-dix (4x20+10)	halvfems (4.5 x "20")	laurogoi ta hamar (4x20+10)
91	novantuno	ninety one	quatre-vingt-onze (4x20+11)	enoghalvfems	aurogoi ta hameka (...+11)
100	cento	hundred (fromhunda-rada: 'the number 100')	cent	hundrede	ehun
1000	mille	thousand (fromthus-hundi: 'swollen hundred')	mille	tusind	mila

Indo-European languages

Non Indo-European languages

Numbers in some synthetic languages...

	Esperanto	Volapük	Interlingua
12 3 4 5 6 7 8 9 10 11 12 13 20 21 22 30 40 50 90 100 1000	unudu tri kvar kvin ses sep ok nau dek dekunu dekdu dektri dudek dudekunu dudekdu tridek kvardek kvindek naudek cento mil	baltel kil pol lul mäl vel jöl zül bals balsebal balsetel balsekil tels telsebal telsetel kils pols luls züls tum balstum	unduo tres quattro cinque sex septe octo novem dece undece duodece tredece vinti vinti-un vinti-duo trenta quaranta cinquanta novanta cento mille

Sunday 24 February 2013

Gaussian Integers

GAUSSIAN INTEGERS

Gaussian integers can be visualized in the complex plane, with their real components on the horizontal axis, and their imaginary components orthogonal along the vertical axis.

[This post is targeted at a level 3 student who has some familiarity with complex numbers.]

Gaussian integers are complex numbers of the form $a+bi,$ where $a$ and $b$ are integers. For example, $2-3i, 4+5i, \ 17,\ 0$ are all Gaussian integers, while $\frac{4}{3}$ , $\sqrt{2}$ , and $-\frac{1}{2}+\frac{\sqrt{3}}{2}i$ are not. One can add, subtract and multiply Gaussian integers just like all other complex numbers. For example:
Addition: $(2-3i)+(4+5i)=6+2i$ ,
Subtraction: $(2-3i)-(4+5i)=-2-8i$ ,
Multiplication: $(2-3i)\cdot(4+5i) = 8+ 10i-12i-15i^2=23-2i$ .

As you can see, the result will again be a Gaussian integer. However, if you try to divide two Gaussian integers, the result will not always be a Gaussian integer:
Division: $\frac{2-3i}{4+5i}=\frac{(2-3i)(4-5i)}{(4+5i)(4-5i)}=\frac{-7-22i}{16+25}=-\frac{7}{41}-\frac{22}{41}i$ .

Like all complex numbers, Gaussian integers have the following properties:

1. The conjugate of $a+bi$ is $\overline{a+bi}=a-bi$ , which is again a Gaussian integer.
2. The norm of $a+bi$ is $N(a+bi)=(a+bi)(a-bi)=a^2+b^2$ , which is a non-negative integer.
3. The absolute value of a Gaussian integer is the (positive) square root of its norm: $|a+bi|=\sqrt{a^2+b^2}$ .
4. There are no positive or negative Gaussian integers, and one cannot say that one is less than another. One can, however, compare their norms.

We say that a Gaussian integer $x$ is a unit, if $\frac{1}{x}$ is also a Gaussian integer. The only units are $1,\ -1,\ i,\ -i$ .

A Gaussian integer $(a+bi)$ is a multiple of a Gaussian integer $(c+di)$ if $(a+bi)=(c+di)\cdot (e+fi)$ for some Gaussian integer $e+fi$ . In this case we say that $c+di$ divides $a+bi$ , and use the notation $(c+di) \mid (a+bi)$ .

A Gaussian integer is called prime, if it is not equal to a product of two non-unit Gaussian integers. It is called composite otherwise. Clearly, multiplying by a unit does not change the primality. Note that the same definition for the usual integers implies that $-5$ is a prime integer. This may seem a bit strange, but no other definition makes sense for the Gaussian integers. (Keep in mind that there is no such thing as a positive Gaussian integer!) Note that a number may be prime as a usual integer, but composite as a Gaussian integer, for example $5=(2+i)(2-i)$ .

There are three kinds of Gaussian primes:
1) $1+i, \ 1-i, \ -1+i,\ -1-i$ . They are all the same up to multiplication by a unit, so we can say $e\cdot (1+i),$ where $e$ is a unit.
2) $e\cdot p$ , where $p$ is a usual prime ( $p\in {\mathbb N}$ ), and $p=4k+3$ .
3) $e\cdot(u+vi)$ or $e\cdot(u-vi)$ , where $u$ and $v$ are natural numbers such that $u^2+v^2=p,$ for a prime $p\in{\mathbb N}$ , $p=4k+1$ . Such $u$ and $v$ exist, and are unique, up to switching $u$ and $v$ , for every prime $p=4k+1$ . This classical result is called the Fermat Two Squares Theorem. It was noticed and announced by Pierre Fermat in 1640 and first proven by Leonhard Euler in 1747.

For those who had learned some abstract algebra, the algebraic properties of Gaussian integers (usually denoted by ${\mathbb Z}[i]$ ) make it a commutative ring, moreover, a domain. Furthermore, just like the usual integers, all Gaussian integers can be decomposed into a product of Gaussian primes, uniquely up to units. The formal way of saying this is that ${\mathbb Z}[i]$ is a unique factorization domain (UFD for brevity).

The classification of Gaussian primes is far from obvious, and so is the unique factorization property. (Speaking of which, do you know how to prove it for the usual integers? You know it to be true from experience, but it is actually not easy to prove!) These theorems will be proven in the upcoming post.

Worked Examples

1. Suppose $n\neq 0$ is a usual integer. Show that a Gaussian integer $a+bi$ is a multiple of $n$ if and only if both $a$ and $b$ are multiples of $n$ .

Solution: By definition, one Gaussian integer is a multiple of the other if and only if their ratio is also a Gaussian integer. Observe that $\frac{a+bi}{n}=\frac{a}{n}+\frac{b}{n}i$ , so $\frac {a}{n}$ and $\frac {b}{n}$ are integers, which means that both $a$ and $b$ are multiples of $n$ .

2. Suppose $a+bi$ is a multiple of $c+di$ . Show that $N(a+bi)$ is a multiple of $N(c+di)$ .

Solution: If $(a+bi)=(c+di)(e+fi)$ , then $(a-bi)=(c-di)(e-fi)$ . Therefore,
$N(a+bi)=(a+bi)(a-bi)=(c+di)(e+fi)\cdot (c-di)(e-fi)=$
$=(c+di)(c-di)\cdot (e+fi)(e-fi) = N(c+di)N(e+fi).$
Because $e$ and $f$ are integers, $N(e+fi)=e^2+f^2$ is an integer.

This is the multiplicative property of the norm, which was mentioned in Complex Numbers Test Yourself 2.

3. Decompose $4+3i$ into a product of primes.

Solution: Because $N(4+3i)=25,$ the norm of any prime that divides $4+3i$ must divide $25$ . Looking at the classification of primes, because $5$ is $1$ modulo $4$ and $5=2^2+1^2$ , there are two such primes, up to units: $2+i$ and $2-i$ . Dividing $4+3i$ by $2+i$ , we get $\frac{11}{5}+\frac{2}{5}i,$ which is not a Gaussian integer. Dividing $4+3i$ by $2-i$ , we get $1+2i=i(2-i)$ . So $4+3i=i(2-i)^2.$

4. Suppose a Gaussian integer $x$ divides a Gaussian integer $y$ . Show that $\bar{x}$ divides $\bar{y}.$

Solution: From Complex Numbers – Worked Example 3, we know that conjugate distributes across multiplication, hence if $y= xz$ , then $\bar{y}=\bar{x}\bar{z}$ .

Give a Try & Test Yourself

1. Show that $1,\ -1,\ i,$ and $-i$ are Gaussian units and there are no other Gaussian units.

2. Find two Gaussian integers that have the same norm and are NOT multiplies of each other, hence the converse of the Example 2 is not true.

3. Show that $1+i$ is a prime. Hint: Norm.

4. Show that every prime integer of the form $4k+3$ is also a Gaussian prime.